1141. Brackets
Sequence
Let us define a regular brackets sequence in the
following way:
1. Empty sequence is a regular sequence.
2. If S is a regular sequence, then (S) and [S] are
both regular sequences.
3. If A and B are regular sequences, then AB is a
regular sequence.
For example, all of the following sequences of
characters are regular brackets sequences:
(), [], (()), ([]), ()[], ()[()]
And all of the following character sequences are not:
(, [, ), )(, ([)], ([(]
Some sequence of characters '(', ')', '[', and ']' is
given. You are to find the shortest possible regular brackets sequence, that
contains the given character sequence as a subsequence. Here, a string a1 a2 ... an is
called a subsequence of the string b1
b2 ... bm, if there exist such
indices 1 ≤ i1 < i2 < ... < in ≤ m, that aj = bij
for all 1 ≤ j ≤ n.
Input. Contains at most 100 brackets (characters '(', ')', '['
and ']') that are situated on a single line without any other characters among
them.
Output. Write a single line that contains some regular
brackets sequence that has the minimal possible length and contains the given
sequence as a subsequence.
Sample Input
([(]
Sample
Output
()[()]
РЕШЕНИЕ
динамическое программирование
Анализ алгоритма
Пусть S = s0s1…sn-1 – входная строка. Пусть dp[i][j] равно наименьшему
количеству символов, которое следует вставить в подстроку si…sj
так чтобы она стала правильной. Очевидно, что dp[i][i] = 1 независимо от
типа скобки si. При i > j положим dp[i][j] = 0. Далее будем писать si ≈ sj, если si – открывающаяся, а sj – соответствующая закрывающаяся скобка.
·
Если si ≈ sj, то dp[i][j]
= min(dp[i][j], dp[i + 1][j – 1]);
·
Если si ≠ sj, то dp[i][j]
= ![]() (dp[i][j], dp[i][k] + dp[k + 1][j]);
(dp[i][j], dp[i][k] + dp[k + 1][j]);
В массиве p будем хранить информацию для восстановления
результирующей строки. Положим
·
p[i][j]
= -1, если si ≈ sj и минимум dp[i][j]
достигается на dp[i + 1][j – 1];
·
p[i][j]
= k, если минимум dp[i][j]
достигается на слагаемом dp[i][k] + dp[k + 1][j];
Пример
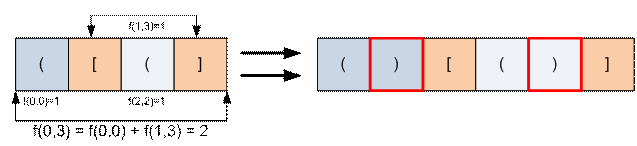
Реализация алгоритма
#include <cstdio>
#include <cstring>
#include <algorithm>
#define MAX 110
#define INF 0x3F3F3F3F
using namespace
std;
char s[MAX];
int dp[MAX][MAX], p[MAX][MAX];
int len;
void Print(int
i, int j)
{
if (i > j) return;
if (i == j)
{
if (s[i] == '(' ||
s[i] == ')')
printf("()");
else
printf("[]");
} else if (p[i][j] ==
-1)
{
printf("%c", s[i]);
Print(i + 1, j -
1);
printf("%c", s[j]);
} else
{
Print(i, p[i][j]);
Print(p[i][j] + 1,
j);
}
}
int Solve(int
i, int j)
{
if (i == j) return 1;
if (i > j) return
0;
if (dp[i][j] != INF) return
dp[i][j];
if ((s[i] == '('
&& s[j] == ')') || (s[i] == '[' && s[j] == ']'))
dp[i][j] =
min(dp[i][j], Solve(i+1,j-1));
for (int k = i; k
< j; k++)
{
int temp = Solve(i,k) + Solve(k+1,j);
if (temp < dp[i][j])
{
p[i][j] = k;
dp[i][j] = temp;
}
}
return dp[i][j];
}
int main(void)
{
gets(s); len =
strlen(s);
memset(dp,0x3F,sizeof(dp));
memset(p,-1,sizeof(p));
Solve(0, len - 1);
Print(0, len - 1);
printf("\n");
return 0;
}